Battle of the Algorithms: Why SGRLD Beats the Competition in GP Inference

Table of Links

Abstract and 1 Introduction

1.1 Methods to handle large spatial datasets

1.2 Review of stochastic gradient methods

2 Matern Gaussian Process Model and its Approximations

2.1 The Vecchia approximation

3 The SG-MCMC Algorithm and 3.1 SG Langevin Dynamics

3.2 Derivation of gradients and Fisher information for SGRLD

4 Simulation Study and 4.1 Data generation

4.2 Competing methods and metrics

4.3 Results

5 Analysis of Global Ocean Temperature Data

6 Discussion, Acknowledgements, and References

Appendix A.1: Computational Details

Appendix A.2: Additional Results

4 Simulation Study

In this section, we test our proposed SGRLD method in (13) method on synthetic data and assess its performance against state-of-the-art Bayesian methods. We use Mean Squared Error (MSE) and coverage of credible intervals of posterior MCMC estimators to evaluate estimation of the spatial covariance parameters, and we use the Effective sample sizes (ESS) (Heidelberger and Welch, 1981) per minute to gauge computational efficiency of MCMC algorithms. We present results only for the spatial covariance parameters θ because the results are similar across methods for β.

4.1 Data generation

4.2 Competing methods and metrics

We compare our SGRLD method with four different MCMC methods. The first three are SG methods with adaptive drifts. The last method uses the full dataset to sample the posterior distribution using the Vecchia approximation. The three SGMCMC methods all use momentum and past gradient information to estimate the curvature and accelerate the convergence. These methods extend the momentum methods used in SG optimization methods for faster exploration of the posterior. The first method is Preconditioned SGLD (pSGLD) of Li et al. (2016a) that uses the Root Mean Square Propagation (RMSPROP) (Hinton et al., 2012) algorithm to estimate a diagonal preconditioner for the minibatch gradient and injected noise. The second method is ADAMSGLD (Kim et al., 2022) that extends the widely used ADAM optimizer (Kingma and Ba, 2014) to the SGLD setting. ADAMSGLD approximates the first-order and second-order moments of the minibatch gradients to construct a preconditioner. Finally, we also include the performance of Momentum SGLD (MSGLD) where no preconditioner is used but past gradient information is used to accelerate the exploration of the posterior. The details of the above algorithms are included in the Appendix A.1. The final method we consider is the Nearest Neighbor Gaussian Process (NNGP) method (Datta et al., 2016). This method is the standard MCMC method based on the Vecchia approximation and is implemented in the R package spNNGP (Finley et al., 2022). For this method, the initial values are set to the true values and the Metropolis-Hastings proposal distribution is chosen adaptively using the default settings.

The prior 90% credible intervals for ρ and ν are (2.06, 7.88) and (0.52, 14.08) respectively, which represent weakly informative priors.

4.3 Results

Table 1 gives the MSE results. Our SGRLD method outperforms all the others with very low MSE across parameters. In particular, the SGMCMC methods all outperform the NNGP method. In our experiments, we noticed that the NNGP method suffers from very slow mixing due to the M-H step necessary for sampling the covariance parameters. In fact, even if we start the

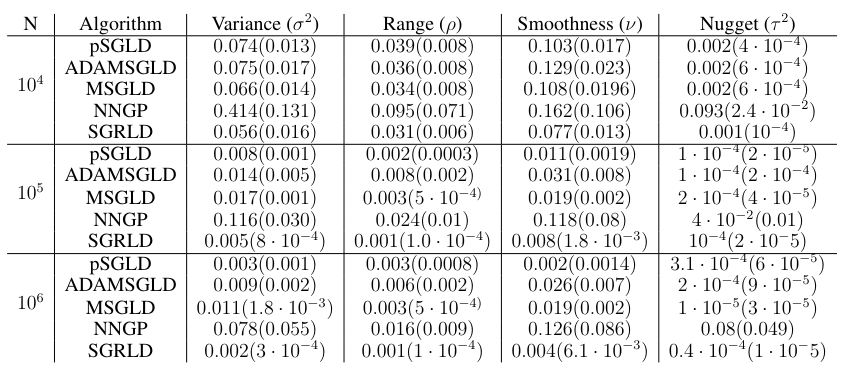
NNGP sampling process at true values of the covariance parameters, and reduce the variance of the proposal distribution, the acceptance rate of the M-H step stays below 15%. None of the SGMCMC methods requires any such step as long as the learning rate is kept small.

For the ESS results in Table 3, the SGRLD method offers superior effective samples per unit time for all the parameters. The pSGLD and MSGLD method seem to adapt to the curvature of the variance parameter, with pSGLD offering higher effective samples than SGRLD. This suggests that the computed preconditioner in pSGLD adapts mainly to the curvature of the variance term,

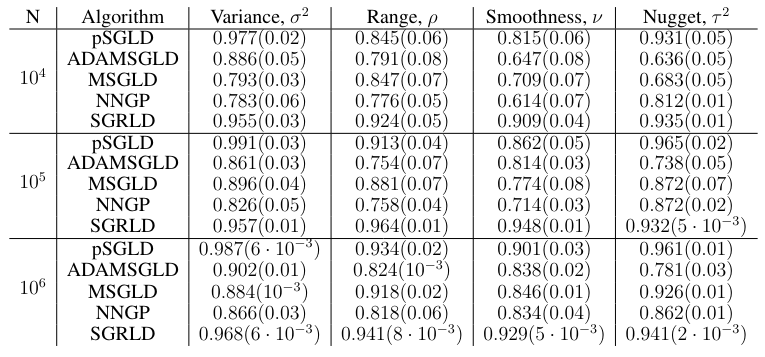
but fails to measure the curvature of the smoothness and range. A similar behavior is also observed in the other two methods, MSGLD and ADAMSGLD. On the other hand, the ESS for SGRLD is of the same order for all the parameters. We believe this indicates that using the Fisher information matrix as a Riemannian metric provides an accurate measure of the curvature and results in higher effective samples for all the parameters. The NNGP method provides low effective sample sizes compared to the other three methods due to the low acceptance rate from the MH correction step.

Given the performance of the SG based methods in this simulation study, especially the SGRLD, we conducted an additional simulation study where we focus on point estimates instead of fully Bayesian inference. In Appendix A.2, we tweak the SGRLD method and turn it into a SG Fisher scoring (SGFS) algorithm for point estimates. We compare this method to the full data gradient Fisher scoring method (Guinness, 2019) already implemented in the GpGp R package (Guinness et al., 2018). We find improved speed and estimation precision compared to the GpGp package.