Application of SGRLD to Large-Scale Ocean Temperature Data: The Argo Case Study

Table of Links

Abstract and 1 Introduction

1.1 Methods to handle large spatial datasets

1.2 Review of stochastic gradient methods

2 Matern Gaussian Process Model and its Approximations

2.1 The Vecchia approximation

3 The SG-MCMC Algorithm and 3.1 SG Langevin Dynamics

3.2 Derivation of gradients and Fisher information for SGRLD

4 Simulation Study and 4.1 Data generation

4.2 Competing methods and metrics

4.3 Results

5 Analysis of Global Ocean Temperature Data

6 Discussion, Acknowledgements, and References

Appendix A.1: Computational Details

Appendix A.2: Additional Results

5 Analysis of Global Ocean Temperature Data

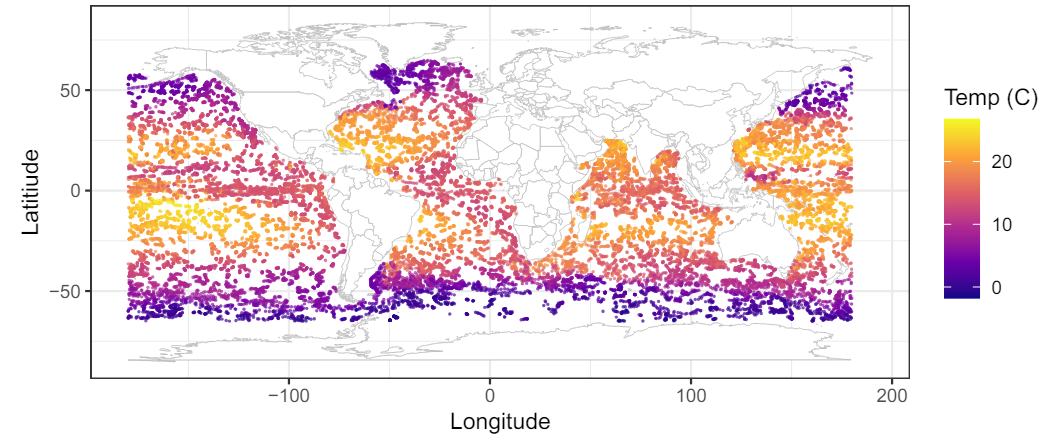
We apply the proposed method to the ocean temperature data provided by the Argo Program (Argo, 2023) made available through the GpGp package (Guinness et al., 2018). Each of the n = 32, 436 observations are taken on buoys in the Spring of 2016. Each observation measures of ocean temperature (C) at depths of roughly 100, 150 and 200 meters. The data are plotted in Figure 1 for depth 100 meters; we analyze these data using the methods evaluated in Section 4. As an illustrative example, the mean function is taken to be quadratic in latitude and longitude and the covariance function is the isotropic Mat´ern covariance function used in Section 4. All prior distributions and MCMC settings are the same as in Section 4.

We first split the data into a test and training set, keeping 20% of the observations in the testing set. We train the models using 8000 and 40000 MCMC iterations for the NNGP ad SGRLD method respectively. For the SGRLD method this requires only 400 epochs. We compare our SGRLD with the NNGP method using prediction MSE, squared correlation between predicted and observed (R2)

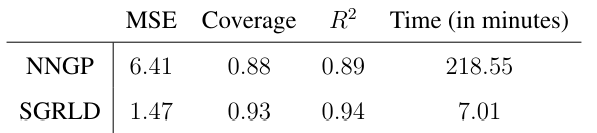
and coverage of 95% prediction intervals on the test set. We also include the effective sample size per minute for all the model parameters.

Table 4 gives the MSE and coverage rate on the testing set, and total training time respectively. Our method achieves less than the quarter of the MSE of NNGP while also requiring less than a twentieth of the time. For the coverage of the 95% prediction intervals, the NNGP method’s average coverage on the testing set is significantly lower than the nominal value, while our proposed method achieves 93% coverage.

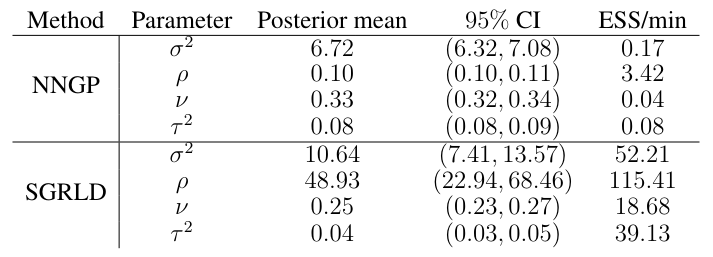
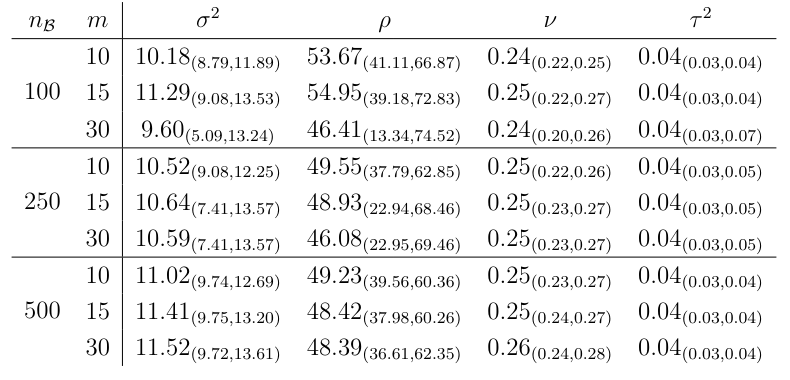
Finally, as a sensitivity analysis, we compare the SGRLD results with mini-batch size nB ∈ {100, 250, 500} and conditioning set size m ∈ {10, 15, 30}. Table 6 show the posterior mean and 95% credible intervals of the covariance parameters for all combinations of the two hyperparameters. The posterior mean of the spatial variance, smoothness and nugget vary little across these combinations of tuning parameters. For the range parameter, we notice a sensitivity to small batch sizes, e.g., nB = 100 resulting in wide credible intervals and larger estimates compared to the other cases. For batch sizes {250, 500} the estimates are similar across values of m.

6 Discussion

SG methods offer considerable speed-ups when the data size is very large. In fact, one can take hundreds or even thousands of steps in one pass through the whole dataset in the time it takes for only one step if the full dataset is used. This enables fast exploration of the posterior in significantly less time. GPs however fall within the correlated setting case where SGMCMC methods have received limited attention. Spatial correlation is a critical component of GPs and naive subsampling during parameter estimation would lead to random divisions of the spatial domain at each iteration. By leveraging the form of the Vecchia approximation, we derive unbiased gradient estimates based on minibatches of the data. We developed a new stochastic gradient based MCMC algorithm for scalable Bayesian inference in large spatial data settings. Without the Vecchia approximation, subsampling strategies would always lead to biased gradient estimates. The proposed method also uses the exact Fisher information to speed up convergence and explore the parameter space efficiently. Our work contributes to the literature on scalable methods for Gaussian process, and can be extended to non Gaussian models i.e. classification.

Acknowledgements

This research was partially supported by National Science Foundation grants DMS2152887 and CMMT2022254, and by grants from the Southeast National Synthesis Wildfire and the United States Geological Survey’s National Climate Adaptation Science Center (G21AC10045).

References

Aicher, C., Ma, Y.-A., Foti, N. J. and Fox, E. B. (2019) Stochastic gradient MCMC for state space models. SIAM Journal on Mathematics of Data Science, 1, 555–587.

Aicher, C., Putcha, S., Nemeth, C., Fearnhead, P. and Fox, E. B. (2021) Stochastic gradient MCMC for nonlinear state space models. arXiv preprint arXiv:1901.10568.

Argo (2023) Argo Program Office. https://argo.ucsd.edu/. Accessed: 2023-11-26.

Baker, J., Fearnhead, P., Fox, E. B. and Nemeth, C. (2019) Control variates for stochastic gradient MCMC. Statistics and Computing, 29, 599–615.

Banerjee, S., Gelfand, A. E., Finley, A. O. and Sang, H. (2008) Gaussian predictive process models for large spatial data sets. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 70, 825–848.

Barbian, M. H. and Assunc¸ao, R. M. (2017) Spatial subensemble estimator for large geostatistical ˜ data. Spatial Statistics, 22, 68–88.

Chee, J. and Toulis, P. (2018) Convergence diagnostics for stochastic gradient descent with constant learning rate. In International Conference on Artificial Intelligence and Statistics, 1476– 1485. PMLR.

Chen, C., Ding, N. and Carin, L. (2015) On the convergence of stochastic gradient MCMC algorithms with high-order integrators. In Neural Information Processing Systems. URLhttps: //api.semanticscholar.org/CorpusID:2196919.

Chen, H., Zheng, L., Al Kontar, R. and Raskutti, G. (2020) Stochastic gradient descent in correlated settings: A study on gaussian processes. Advances in neural information processing systems, 33, 2722–2733.

Chen, T., Fox, E. and Guestrin, C. (2014) Stochastic gradient Hamiltonian Monte Carlo. In International conference on machine learning, 1683–1691. PMLR.

Cressie, N. (1988) Spatial prediction and ordinary kriging. Mathematical geology, 20, 405–421.

Cressie, N. and Johannesson, G. (2008) Fixed rank kriging for very large spatial data sets. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 70, 209–226.

Dalalyan, A. S. and Karagulyan, A. (2019) User-friendly guarantees for the Langevin Monte Carlo with inaccurate gradient. Stochastic Processes and their Applications, 129, 5278–5311.

Datta, A., Banerjee, S., Finley, A. O. and Gelfand, A. E. (2016) Hierarchical nearest-neighbor Gaussian process models for large geostatistical datasets. Journal of the American Statistical Association, 111, 800–812.

Dubey, K. A., J Reddi, S., Williamson, S. A., Poczos, B., Smola, A. J. and Xing, E. P. (2016) Variance reduction in stochastic gradient Langevin dynamics. Advances in neural information processing systems, 29.

Durmus, A. and Moulines, E. (2017) Nonasymptotic convergence analysis for the unadjusted ´ Langevin algorithm. The Annals of Applied Probability, 27, 1551 – 1587. URLhttps: //doi.org/10.1214/16-AAP1238.

Finley, A. O., Datta, A., Cook, B. D., Morton, D. C., Andersen, H. E. and Banerjee, S. (2019) Efficient algorithms for Bayesian nearest neighbor Gaussian processes. Journal of Computational and Graphical Statistics, 28, 401–414.

Furrer, R., Genton, M. G. and Nychka, D. (2006) Covariance tapering for interpolation of large spatial datasets. Journal of Computational and Graphical Statistics, 15, 502–523.

Gelfand, A. E. and Schliep, E. M. (2016) Spatial statistics and Gaussian processes: A beautiful marriage. Spatial Statistics, 18, 86–104. URLhttps://www.sciencedirect.com/ science/article/pii/S2211675316300033. Spatial Statistics Avignon: Emerging Patterns.

Guhaniyogi, R. and Banerjee, S. (2018) Meta-kriging: Scalable Bayesian modeling and inference for massive spatial datasets. Technometrics.

Guinness, J. (2018) Permutation and grouping methods for sharpening Gaussian process approximations. Technometrics, 60, 415–429. URLhttps://doi.org/10.1080/00401706. 2018.1437476. PMID: 31447491.

— (2019) Gaussian process learning via fisher scoring of vecchia’s approximation.

Guinness, J., Katzfuss, M. and Fahmy, Y. (2018) Gpgp: fast Gaussian process computation using Vecchia’s approximation. R package version 0.1. 0.

Hardt, M., Recht, B. and Singer, Y. (2016) Train faster, generalize better: Stability of stochastic gradient descent. In International conference on machine learning, 1225–1234. PMLR.

Heaton, M. J., Datta, A., Finley, A. O., Furrer, R., Guinness, J., Guhaniyogi, R., Gerber, F., Gramacy, R. B., Hammerling, D., Katzfuss, M. et al. (2019) A case study competition among methods for analyzing large spatial data. Journal of Agricultural, Biological and Environmental Statistics, 24, 398–425.

Heaton, M. J. and Johnson, J. A. (2023) Minibatch Markov chain Monte Carlo algorithms for fitting Gaussian processes. arXiv preprint arXiv:2310.17766.

Heidelberger, P. and Welch, P. D. (1981) A spectral method for confidence interval generation and run length control in simulations. Communications of the ACM, 24, 233–245.

Hinton, G., Srivastava, N. and Swersky, K. (2012) Neural networks for machine learning lecture 6a overview of mini-batch gradient descent. Cited on, 14, 2.

Kang, E., Liu, D. and Cressie, N. (2009) Statistical analysis of small-area data based on independence, spatial, non-hierarchical, and hierarchical models. Computational Statistics & Data Analysis, 53, 3016–3032.

Katzfuss, M. and Cressie, N. (2011) Spatio-temporal smoothing and em estimation for massive remote-sensing data sets. Journal of Time Series Analysis, 32, 430–446.

Katzfuss, M. and Guinness, J. (2021) A general framework for Vecchia approximations of Gaussian processes. Statistical Science, 36, 124–141.

Kaufman, C. G., Schervish, M. J. and Nychka, D. W. (2008) Covariance tapering for likelihoodbased estimation in large spatial data sets. Journal of the American Statistical Association, 103, 1545–1555.

Kim, S., Song, Q. and Liang, F. (2022) Stochastic gradient Langevin dynamics with adaptive drifts. Journal of statistical computation and simulation, 92, 318–336.

Kingma, D. P. and Ba, J. (2014) Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980.

Li, C., Chen, C., Carlson, D. and Carin, L. (2016a) Preconditioned stochastic gradient Langevin dynamics for deep neural networks. In Proceedings of the AAAI conference on artificial intelligence, vol. 30.

Li, W., Ahn, S. and Welling, M. (2016b) Scalable MCMC for mixed membership stochastic blockmodels. In Artificial Intelligence and Statistics, 723–731. PMLR.

Ma, Y., Ma, Y.-A., Chen, T. and Fox, E. B. (2015) A complete recipe for stochastic gradient MCMC. In Neural Information Processing Systems. URLhttps://api. semanticscholar.org/CorpusID:17950949.

Ma, Y.-A., Foti, N. J. and Fox, E. B. (2017) Stochastic gradient MCMC methods for hidden Markov models. In International Conference on Machine Learning, 2265–2274. PMLR.

Mardia, K. V. and Marshall, R. J. (1984) Maximum likelihood estimation of models for residual covariance in spatial regression. Biometrika, 71, 135–146. URLhttp://www.jstor.org/ stable/2336405.

Nemeth, C. and Fearnhead, P. (2021) Stochastic gradient Markov chain Monte Carlo. Journal of the American Statistical Association, 116, 433–450. URLhttps://doi.org/10.1080/ 01621459.2020.1847120.

Newton, D., Yousefian, F. and Pasupathy, R. (2018) Stochastic gradient descent: Recent trends. Recent advances in optimization and modeling of contemporary problems, 193–220.

Robbins, H. and Monro, S. (1951) A Stochastic Approximation Method. The Annals of Mathematical Statistics, 22, 400 – 407. URLhttps://doi.org/10.1214/aoms/1177729586.

Roberts, G. O. and Rosenthal, J. S. (1998) Optimal scaling of discrete approximations to Langevin diffusions. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 60. URLhttps://api.semanticscholar.org/CorpusID:5831882.

Rue, H., Martino, S. and Chopin, N. (2009) Approximate Bayesian inference for latent Gaussian models by using integrated nested laplace approximations. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 71, 319–392.

Saha, S. and Bradley, J. R. (2023) Incorporating subsampling into Bayesian models for high-dimensional spatial data. arXiv preprint arXiv:2305.13221.

Sang, H., Jun, M. and Huang, J. Z. (2011) Covariance approximation for large multivariate spatial data sets with an application to multiple climate model errors. The Annals of Applied Statistics, 2519–2548.

Stein, M. L. (1999) Interpolation of spatial data: some theory for kriging. Springer Science & Business Media.

— (2002) The screening effect in Kriging. The Annals of Statistics, 30, 298 – 323. URLhttps: //doi.org/10.1214/aos/1015362194.

— (2011) 2010 Rietz lecture: When does the screening effect hold? The Annals of Statistics, 39, 2795–2819. URLhttp://www.jstor.org/stable/41713599.

Stein, M. L., Chi, Z. and Welty, L. J. (2004) Approximating likelihoods for large spatial data sets. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 66, 275–296.

Teh, Y., Thiery, A. and Vollmer, S. (2016) Consistency and fluctuations for stochastic gradient ´ Langevin dynamics. Journal of Machine Learning Research, 17.

Vecchia, A. V. (1988) Estimation and model identification for continuous spatial processes. Journal of the Royal Statistical Society: Series B (Methodological), 50, 297–312.

Welling, M. and Teh, Y. W. (2011) Bayesian learning via stochastic gradient Langevin dynamics. In International Conference on Machine Learning. URLhttps://api.semanticscholar. org/CorpusID:2178983.

Woodard, R. (2000) Interpolation of spatial data: some theory for kriging. Technometrics, 42, 436.

Appendix A.1: Computational Details

Here we give the detailed algorithms of the SG methods with adaptive drifts. The RMSprop (Root Mean Square Propagation) algorithm is an optimization algorithm originally developped for training neural networks models. It adapts the learning rates of each parameter based on the historical gradient information. This can be seen as adaptive preconditioning method.

Momentum SGD is an optimization algorithm that uses a Neseterov momentum term to accelerate the convergence in the presence of high curvature or noisy gradients. Momentum SGD proceeds as follows

The Adam algorithm combines ideas from RMSprop and momentum to adaptively adjust learning rates.

Appendix A.2: Additional Results

Maximum likelihood estimates

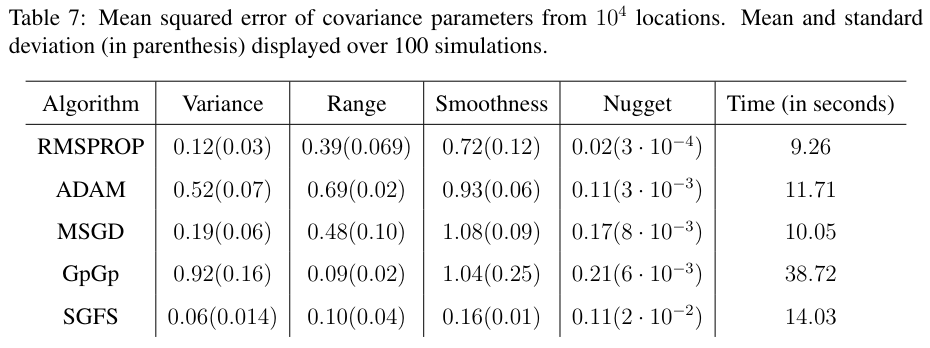
The results in Table-7 show that the SGFS outperforms the other methods in terms of estimation error. Compared to GpGp, the stochastic methods take at most half the time while performing twenty times more iterations.